コロナ予報（COVID-19Forecast)　

•コロナ予報 （COVID-19 Forecast)について

•SIQRモデルとその係数の決め方（その2）

・隔離率q’と感染率β’の効果について　他

新型コロナウイルス感染症数理モデル研究会

新型コロナウイルス感染拡大の予測　並木正夫

更新 2020.08.23

 

コロナ予報 は、8月4日から研究会のHPで公開しました。

新しいデータを取り込んで8月6日、9日、13日、16日、19日に更新をしました。8月4日の予報では、ピークが7月末から8月下旬と地域によって差がありました。データが集まった19日の予報では、神奈川県を除く他の地域は、8月初めまでにピークアウトしています。8月22日のデータでは、 1日の新規感染者は、神奈川県もピークを迎えています。8月20日、政府の分科会の尾身会長が講演を行い「東京や沖縄、大阪などでは医療機関への負荷が大きい状況が続いているが、今の流行は全国的にはだいたいピークに達したというのが私たちの読みだ。今後の推移を注意深く見守っていく必要がある。・・・」と述べました。

☞PDF ZOOM Mtg プレゼン資料200823_2R

 

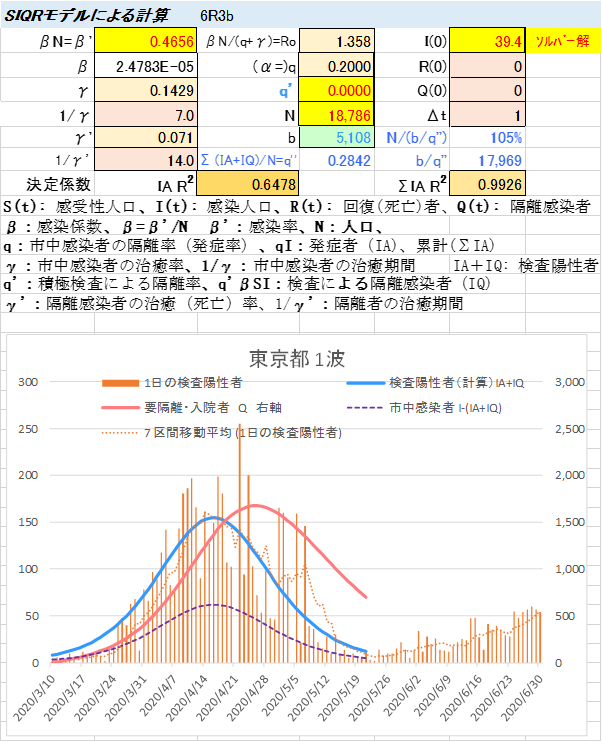
ここに掲げた図は、コロナ予報から東京都の図を抜き出して並べたものです。

予報は、公開した8月4日からほとんど同じなので、遅くも8月4日には、日々公表される1日の新規感染者や入院・療養が必要な感染者の数を予測できていました。

東京都の場合、入院・療養者（入院が必要な感染者は、この半分）のピークは8月14日なっていますから10日前には正確な数字を予測していたことになります。

10日前が充分に早いとは思いませんが、台風の予報より余裕がありそうです。

残念ながら、関係者にこの情報は届いていないので、お役に立ってはいません。

コロナ予報では、途中から入院・療養者の予測を追加しています。

入院・療養者（要隔離・入院者）は、SIQR方程式のQをプロットしたものです。

Qに係わる、隔離者の治癒期間1/γ‘は、都合がいいことに、1日の新規感染者（IA+IQ)の計算結果には影響しないので、必要に応じて公表される入院・療養者のデータに合わせて調整します。東京都の場合は、当初14日としていたものを13日にしています。

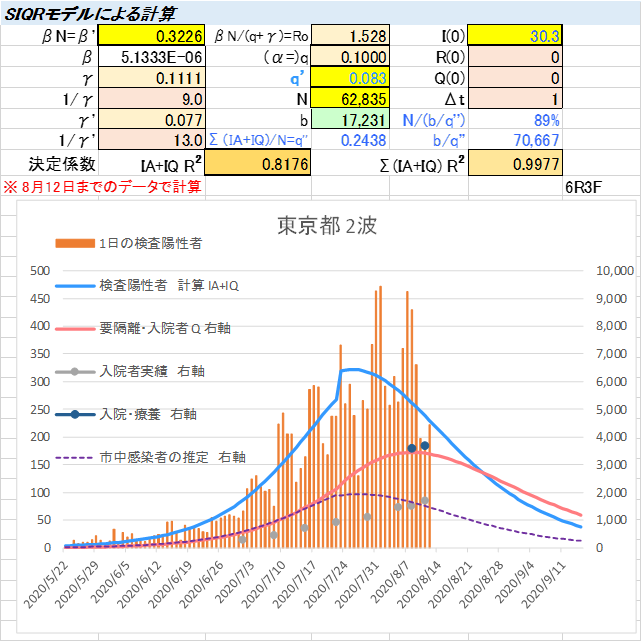
• 感染日ベースでは既にピークを越えたと見られます
• 入院・療養者のピークは8月末で、18,000人まで増えると予測しています
• 図中の要隔離・入院者と入院・療養者は同じ意味です

東京ではピークに近づいている。入院・療養者数のピークは8/21頃で、4,000人を超える見込み。現在の入院者は、要隔離・入院者の半分。

 

医療崩壊を起こさないためには、入院・療養者（要隔離・入院感染者）の予測が重要！隔離感染者の治癒期間1/γ‘は、検査陽性者の計算結果に影響を与えないので、ハイパーパラメータとして要隔離・入院者のカーブが実データに合うように調整する

大阪府では、重症者が増えていて、重症者用に確保してある病床数188を越えるのではないかと危機感を持っています。21日、確保しようとしている重症者用の病床を含めた215の病床数を9月9日に越える可能を心配していました。

どんな計算で9月9日までの予測をしたかわかりませんが、指数関数で回帰したのなら過大に計算したことになります。重症者になる条件が16日までの状況とほぼ同じなら、予報のような推移をとるはずです。従って、重症者用の病床は、現有の188床で足りることになります。

重症者は入院期間が長くなるので、その分を考慮する必要があると考えていましたが、死亡者がデータから抜けて行くためか、Qに地域ごとの重症者の比率を掛けるだけでカーブフィットしています。

大阪府の新規感染者、要隔離・入院者も既にピークを越えたように見えます

実効再生産数Reは、全国では8月11日に、大阪では、8月9日に1を切りました。

大阪では、1日の新規感染者が100人を、あるいは50人を切るのがいつ頃かを話題にしてもいいはずですが、1日の感染者のピークを過ぎたとは言いません。

重症者が増えていることは問題ですが、新規感染者のピークに遅れて、重症者のピークも来ます。という事で、重症者の予測を計算しました。

 

 上の図、重症者の予測は、Qに重症者の比率を掛けて、重症化までの期間を考慮して横にシフト。近い結果になると考えている。

 

• SIQR数理モデル方程式の係数は6つ。SIQRの初期値を入れて10。
  S(0),Q(0),R(0)=0とすれば、変数は7つ。（※）
• SIQR方程式を回帰方程式と考えれば、決定係数の計算式が目的関数になり、係数と初期値はその説明変数になる
• これを全てExcelのソルバーに任せると、もっともらしい答えが見つかる場合もある
• ソルバーは、決定係数が最大になるように、説明変数の組み合わせを探すが、近くの極を探すので、初期値によって答えが異なる場合がある(右図）
• データが少ない（感染初期）と過学習（オーバー・フィッティング）になりやすい
• 過学習を防ぐ方法は、
  • データの数を増やす
  • ハイパーパラメータを調整する
  • 正則化する
• 自粛に関係するβ’は、結果にセンシティブだが、良く分からないのが実状
• 実効感染機会人口Nは、クラスターが集合した数字だが、これも良く分からない

良く分からないものは、第1波の解析結果を利用するか、ソルバーに任せる

• ロジスティック曲線回帰なら変数は3つ
  y = b/(1+c*exp(-ax))
• 指数関数なら2つ（区間限定しか使えない）
  y=I(0)*exp(λ*ｘ）　　 

大阪府では、「重症者が、このまま増えれば9月9日に215を超える」との発言も(8/20) 

dS(t)/dt= -β*S(t)*I(t)

dI(t)/dt=(1-q')*β*S(t)*I(t)-γ*I(t)-q*I(t)

　           IA(t)=q*I(t)（確定感染者、発症者）、ΣIA：累計感染者

              dQ(t)/dt= q'*β*S(t)*I(t)+q*I(t)-γ'*Q(t)

              dR(t)/dt=γ*I(t)+γ'*Q(t)

　N=S(t)+I(t)+Q(t)+R(t)

S(t):未感染者、I(t): 市中感染者、R(t): 回復(死亡)者、Q(t):要隔離感染者

β：感染係数、β=β'/N　β':感染率、N：人口（実効感染機会人口を使う）

q：市中感染者の隔離率（発症率）、qI：隔離者（発症者）（=IA）

γ：市中感染者の治癒率、1/γ：市中感染者の治癒期間、γI：市中の治癒者

q'：積極検査による隔離率、q'βSI：検査による隔離感染者（=IQ）

　（qI+q'βSI）：1日の検査陽性者（=IA+IQ）‥‥　公表される感染者

γ'：隔離感染者の治癒率（死亡者を含む）、1/γ'：隔離者の治癒期間

ここからは、前回のZOOM Mtg.と重複しますが、前回説明しきれなかった点を補足します。前回、まとめとしたスライド「６．AI（機械学習）の問題点」で、過学習を防ぐ方法として②、③を中心に検討すると書きました。

②については、スライド4で述べたように、隔離者の治癒期間1/γ‘は、ハイパーパラメータとすることが出来ます。

➂の正則化とは係数に制限を加えることですが、以下のスライドで説明します。

このスライドは、SIQR方程式の隔離率（発症率）q、治癒率γ、感染率β’、実効感染機会人口Nの関係を東京都の第1波の例で調べたものです。

表Aに示すようにどの組み合わせでも決定係数R2は、ほとんど同じです。

図Aは、ｑとNの関係で、隔離率は、当初0.2程度と聞いていましたが、もう少し低いという意見もあります。治癒率が同じならq=0.1~0.2では、Nはあまり変わりません。

治癒期間1/γも9日から14日程度と言われているので、東京都の場合N=12,000~20,000に収まりそうです。

図Bは、治癒期間1/γと感染率β‘の関係です。治癒期間9日~14日で、ｑ＝0.1~0.2では、β’＝0.3~0.45に収まりそうです。

図Cは、治癒期間1/γと実効感染機会人口Nの関係です。ｑ＝0.1~0.2では、N＝12,000~20,000に収まりそうです。

感染の初期で、データが少ない時に、これらの結果を使って、β’、ｑに制限を設けるとソルバーの解が安定します。

 

 このスライドは、隔離率ｑを変化させたときの計算です。

隔離率qを変えると市中感染者の推定値は変化しますが、都合がいいことに1日の新規感染者や入院・療養者は変化しません。

市中の感染者は、1日の新規感染者（陽性者）が発症者と未発症者を区別したデータが公表されていれば、もう少し推定の精度を上げることは可能と思いますが、今のところ、このデータは入手できないので参考に計算しています。

 隔離率qを変えると市中感染者の推定値は変化するが、1日の新規感染者や入院・療養者は変化しない！

このスライドの下から2つの図は、治癒期間1/γを変化させたときの計算です。都合がいいことに、Nは変化しますが1日の新規感染者（青の曲線）や入院・療養者（赤の曲線）は変化しません。

下の図は、隔離感染者の治癒期間を変えた時の入院・療養者の変化です。

3つの図ともNは、ソルバーが求めています。

 

市中感染者の治癒期間1/γを変えるとＮは変化するが（P７参）、

1日の新規感染者や入院・療養者は変化しない！

隔離感染者の治癒期間1/γ’を変えると要隔離・入院者Ｑは変化する 

このスライドは、第1波と第2波で実効感染機会人口Nをソルバーで求めさせた結果とロジスティック曲線回帰で求めた累計感染者bを表にしたものです。

東京都の場合、第2波は第1波の規模(累計）の3倍以上、ピーク(7日間移動平均が近い）で2倍以上になります。

ロジスティック曲線回帰では、実効感染機会人口は使いませんし、求まりません。累計のS字カーブのt=∞のbが計算されます。

SIQR方程式でも、累計の感染者Σ(IA+IQ)を計算しているので、この値が落ち着いた時のｑ‘’＝Σ(IA+IQ)／Ｎを計算しています。

従って、ｂ／ｑ‘’ がＮと同じになるはずです。Ｎ／（ｂ／ｑ‘’）の右横のセルが、その差をチェックしているセルです。±10%に収まればいいことにしています。

東京都、8月15日までの累計感染者

17,454人

• 人口Nを行政区画に対応させて決めることは、感染拡大のメカニズムから考えれば合理的とは言えない
• 計算も首都圏で計算するならまだしも東京都だけで計算することに合理性はあるか？
• 実際のデータは、行政区画ごとに集計され、入院・療養も行政区画ごとの対応になるので、実務的な妥協をしたということ

 

 同じ感染の期間でも、感染エリアが広がるのでNは変化すると考えられるが、その期間の平均で計算していることになる

 

 

東京都の新型コロナウイルス感染者の分布マップ（市区町村別） 

https://graph-stock.com/map/covid19-confirmed-cases-in-tokyo/

 このスライドは、ＰＣＲ検査を積極的に行って市中の感染者を隔離した時の効果を模擬したものです。下の図を基準として、中央の図は、市中の不顕性感染者の隔離率q‘をピークの直前で2倍にしたもの。（不顕性感染者の隔離率を2倍にしたもので、PCR検査隔離人数を2倍ではない。）当然、増やした瞬間に1日の新規感染者は増えるが、その後の新規感染者もほとんど減らない。右の図は、感染の初期にq’を2倍にしたもので、新規感染者も増えず、ピークが後ろ倒しになって減る。

 7/23から各利率ｑ’を2倍　効果は少ない

不顕性感染者の隔離率q’を2倍にしたもので、PCR検査隔離人数が2倍ではない

  7/23から各利率ｑ’を2倍　効果は大きい

不顕性感染者の隔離率q’を2倍にしたもので、PCR検査隔離人数が2倍ではない

• 感染の初期（感染拡大が始まる前）のPCR検査・隔離が有効
• これまでは、感染が減るとPCR検査人数も減っていた。感染鎮静時の検査が効果大

 

 

このスライドは、首都圏と近畿圏の2週間毎のPCR検査人数です。どこの地域でも感染の初期の検査人数が少ない。

PCR検査は、一番効果があると思われる時期に少なかった 

このスライドは、自粛要請のタイミングの効果を模擬したものです。

感染率β’を±10%変動させて、自粛率の模擬をしたもの。

感染の初期の対応が重要であることが模擬できる。

矢印（↓）の時点で感染率β’を±10%変化させたときのその後の予測（シミュレーション）　

東京都の場合（8/12までのデータで実施）

 【効果は大きい！】

7/2　都で2カ月ぶりに100人越え、 都知事は、『感染拡大要警戒』の段階にあると認識」

7/15  都知事は、「警戒レベル引き上げ（感染拡大警報）」

7/17  専門家は、「患者の増加スピードが病床数を上回りそうで危惧」

7/22　Go To トラベル 開始

【効果は減る】

7/23  都知事は、「4連休は外出控えて」（新規感染者366人を受け）

8/1    都で、1日の新規感染者が最高の472人を記録 

 【効果は少ない】 

8/6    都知事は、「お盆や夏休み期間の都外への旅行・帰省控えて」

8/14  都HPでは、「感染が拡大していると思われる」「医療体制強化が必要と思われる」

https://www3.nhk.or.jp/news/special/coronavirus/data/

3． 自粛の効果を推測できる（β’の変化）

詳細はこちらのPDFを参照してください

☞PDF ZOOM Mtg プレゼン資料200823_2R